1. 相关概念

use::轮换算法

2. 描述：

快速排序采用递归的方法，属于[father::分治法]

3. 适用范围：

3.1. 应用场景:

需要第一梯队的排序效率时
记录数量较多
1. 一般来说, 记录数量大于7时, 快速排序才有优势
稳定要求不高

优点:

第一梯队的速度
1. 比堆排序快一点

3.2. 缺点:

不稳定排序
速度不太稳定, 不过可以接受
需要占用函数栈空间

3.3. 最坏情况:

当数据已经有序时此时时间复杂度为O (n²)

3.4. 最好情况:

每次基准值都能取到数据的中位数

4. 原理：

第一次，在数列中随机选取一个基准数值，然后把数列分成两部分，左边小于等于基准值，右边大于基准值，然后递归的对这两部分再次快速排序，出口为数列不存在或数列中只有一个数

5. 快速排序的优化

优化快速排序的基准点取值: 三字取中法
1. 即在头尾中三个关键字中选中值作为基准点
用插入排序代替快速排序来排序少量记录

6. 伪代码：

6.1. 双/二路快速排序:

//将A[a...b]进行排序  
function QUCKSORT(A, a, b)  
if b<=a //设置数列不存在或只有一个数为出口  
return  
q = PARTITION(A, a, b)  //q 作为分界点, 后面需要用到, 先存起来
QUCKSORT(A, a, q-1)  
QUCKSORT(A, q+1, b)  
 
//将A[a..b]进行随机划分  
function PARTITION(A, a, b)  
p = [a, b]之间的随机整数//或p = a  
SWAP(A[p], A[b])  
i = a  
for j = a to b-1  
if A[j]<=A[b]  
SWAP(A[i], A[j])  
i = i+1  
SWAP(A[i], A[b])  
return i

7. 在c语言中的实现

7.1. 挖空/原始/普通快速排序:

梗概:

根据基准值划分
1. 使用双指针把数组划分为三个区域: 左边为小数, 右边为大数, 中间为未划分
2. 采用轮换算法交换大数和小数到对应区域中代码:

void swap(RecordType Records[],int i,int j){
	RecordType temp=Records[i];
	Records[i]=Records[j];Records[j]=temp;
}
int Partition(RecordType Records[],int low, int high){
	/*先要空出一个位置,用来轮换多个记录的位置*/
	RecordType point=Records[low];//此时low指向无意义的记录
	while(low<high){
		/*延拓大数区域,直到遇到不该于此的小数,此时high指向小数*/
		for(;low<high && Records[high].key>=point.key;--high);
		/*把high所指记录移到low指向的空位,此时high指向空位*/
		Records[low]=Records[high];
		/*延拓小数区域,直到遇到不该于此的大数,此时low指向小数*/
		for(;low<high && Records[low].key<=point.key;++low);
		/*把low所指记录移到high指向的空位,此时low指向空位*/
		Records[high]=Records[low];
	}
	/*轮换完成,用基准记录把最后low所指的空位填上*/
	Records[low]=point;
	return low;
}
 
void QKSort(RecordType records[],int low,int high){
	if(low<high){
		int pos=Partition(records,low,high);
		QKSort(records,low,pos-1);
		QKSort(records,pos+1,high);
	}
}

7.2. 双/二路快速排序:

7.2.1. 梗概:

7.2.1.1. 快速排序：

对数列闭合区间a到b进行划分，把基准值记录为p，把小于等于p的数都放到p的左边, 大于p的数放在p的右边, 这时候p就不用管了, 只需要对左边和右边分别用快速排序排好序就行了，这时就使用到递归了(自己调用自己), 出口为数列不存在或数列中只有一个数(不需要排序, 已经有序了)

7.2.1.2. 划分：

重点是划分成两部分 对于所用情况，我们先从一般开始, 以这个一般方法为主体再考虑特殊情况, 然后针对特殊情况对一般方法做改进

7.2.1.2.1. 大数小数都有,且处于中期阶段(一般方法)(方法主体)

先不管循环体的具体的开始操作和结束操作, 等到后面处理特殊情况的时候再考虑

假设基准值可将数列分为大数部分和小数部分

先将基准值放在最右边(方便处理, 后面等把大数小数都划分清楚了, 直接放在中间, 就非常好处理)，然后把这个数列看作三个部分，如图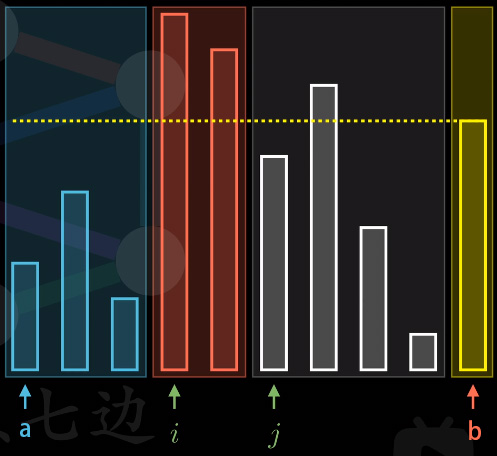：都是左闭右开的区间(因为c语言习惯使用左闭右开, 其实其他形式的区间也是可以的, 只不过实现方法不同罢了)，蓝色为小的那部分，红色为大的那部分，灰色为待区分的那部分。i指向大数的第一个，j指向待划分的第一个，注意这个大数部分的变化类似于窗口滑动。而j作为待划分部分的第一个元素，同时也是大数窗口的右边界。
假设一次遍历内容开始的时候，判断j指针指向的未划分数
1. 如果新数是大数，因为大数区间紧挨着为划分区间, 所以直接把大数区间往右覆盖一位(j右移), 大数+1, 未划分数-1
2. 如果新数是小数, 我们目标是将小数放到小数窗口内。又因为窗口是连续性地滑动的，那小数窗口势必会覆盖大数窗口的左边第一位，这个位置我们就可以把大数拿走，让给小数，而这个大数我们可以放在j指向的空位。即交换j和i所指向的数值。然后小数窗口往右拓展一位(i后移一位)，以占用大数窗口第一位，小数+1, 大数-1. 为了复原大数区域, 把j往后移一位, 大数+1.
经过上一步, 无论如何, j都会往后一步, 所以就完美衔接遍历开始了, 所以j后移就是遍历的结束

7.2.1.2.2. 大数小数都有,且处于末尾阶段

假设此时j位于倒数第二个数
按照上面情况的处理方法, 划分该数之后, j后移一位, 指向了基准值
此时整个遍历循环终结了, 需要对结果进行处理
1. 把基准值p放到大数和小数中间
  1. 因为大数和基准值p是连着的, 所以应该针对大数区域入手
  2. 把大数区域整体往右移动, 大数-1, 中间空位+1
  3. 把空位上的大数和基准值互换, 大数+1, 中间空位-1, 中间数+1
2. 因为还需要对大数和小数分别再细分, 需要用到p作为边界, 所以把p返回

7.2.1.2.3. 初始阶段

刚开始刚开始只有待划分部分，而小数和大数部分窗口长度都为0，则a和i都在同一位置，这样小数窗口长度为0，i和j在同一位置，这样大数窗口长度为0.

开始的时候j指向第一个元素, 同时是第一个未划分元素, 所有需要对其进行划分
比较j指针指向的元素
1. 如果为大数, j往后移动, 大数区间(i与j的左闭右开区间)自然就会包括该大数, 大数+1, 为划分数-1
2. 如果为小数
  1. 则小数区间向右扩展, 即i向右移, 小数+1, 大数区间长度为-1
  2. 然后j再往右移一格, 未划分数-1, 大数区间长度+1=0
我们发现这就与初始阶段的操作对应了,且与中期阶段的操作也对应了,则一般方法不用改进. 而且我们就确定了循环以判断j为开始, 以移动j为结束

7.2.1.2.4. 只有大数的情况

先假设从一开始到中间, 都只有大数
1. 那么按照初始阶段和中间阶段的处理方法, a和i会一直停留再第一个元素上
再假设从中间到结束, 都只有大数
1. 由上面的假设得a和i一直在第一个元素上, 按照末尾阶段的移动j方法, j最后会停在最后一个元素上, 即基准值上
  1. 按照末尾阶段的交换方法, 基准值和i指向的元素互换
  2. 此时,基准值放在第一个, 同时也是大数区域的左边, 合理
发现一般方法能够应对, 无需改进

7.2.1.2.5. 只有小数的情况

假设从一开始到中间, 都只有小数
1. 按照初始阶段到中间阶段的处理方法,j和i一直指向同一个元素
假设从中间到结束,都只有小数
1. 按照结束阶段的处理方法
  1. i和j指向基准值上
  2. 将j和i指向的元素互换
  3. 则基准值位置不变, 刚好处于小数区域的右边, 合理
  4. 故一般方法适用于该特殊情况, 不用改进

7.2.1.2.6. 最特殊的情况: 传给划分操作的数组只有两个数

随便选取一个基准值后, 待划分数只有一个
按照初始的处理方法和, 判断j
1. 如果为大数, j往后移动, 大数区间(i与j的左闭右开区间)自然就会包括该大数, 大数+1, 未划分数-1
2. 如果为小数
  1. 按照只有小数的情况进行处理
  2. 发现i和j指向了基准值上
  3. 且i和j所指的值互换后, 合理
3. 如果为大数
  1. 按照只有大数的情况进行处理
  2. 最后基准值会和这个大数互换, 合理
综上, 合理, 无需改进一般方法

以上，包含了所有需要划分的情况，划分完成

7.2.2. 代码:

//划分数组
int PARTITION(int *A, int a, int b) {  
int p, temp, i, j;  
p = a;  
temp = A[p];  
A[p] = A[b];  
A[b] = temp;  
i = a;  
for (j = a; j <= b - 1; ++j) {  
if (A[j] <= A[b]) {  
temp = A[i];  
A[i] = A[j];  
A[j] = temp;  
++i;  
}  
}  
temp = A[i];  
A[i] = A[b];  
A[b] = temp;  
return i;  
}
//递归快速排序
void QUICKSORT(int *A, int a, int b) {  
int q;  
if (b <= a)  
return;  
q = PARTITION(A, a, b);  
QUICKSORT(A, a, q - 1);  
QUICKSORT(A, q + 1, b);  
}

7.3. 优化快速排序:

梗概:

使用三数取中法+插入排序补充代码:

#define MIN_CONDITION 7//记录长度小于该值,使用插入排序
void swap(RecordType Records[],int i,int j){
	RecordType temp=Records[i];
	Records[i]=Records[j];Records[j]=temp;
}
int BettPartition(RecordType Records[],int low, int high){
	/*三字取中法*/
	int mid = (low+high)>>1;
	/*排成升序: mid low high*/
	if(Records[mid].key>Records[high].key)swap(Records,mid,high);
	if(Records[low].key<Records[mid].key)swap(Records,low,mid);
	if(Records[low].key>Records[high].key)swap(Records,low,high);
	/*先要空出一个位置,用来轮换多个记录的位置*/
	RecordType point=Records[low];//此时low指向无意义的记录,作为空位
	while(low<high){
		/*以下两个for分别找出左边的大数,以及右边的小数,然后移到正确的位置*/
		for(;low<high && Records[high].key>=point.key;--high);
		/*把high所指记录移到low指向的空位,此时high指向空位*/
		Records[low]=Records[high];
		for(;low<high && Records[low].key<=point.key;++low);
		/*把low所指记录移到high指向的空位,此时low指向空位*/
		Records[high]=Records[low];
	}
	/*轮换完成,用分界记录把最后low指向的空位填上*/
	Records[low]=point;
	return low;
}
 
void inser_sortInQK(RecordType records[],int low,int high){
	int i,j;
	RecordType temp;
	for (i=low+1;i<=high;i++){//从第二个开始遍历
		temp = records[i];//为轮换空出位置
		/*给temp腾出位置,集体向后轮换*/
		for(j=i-1;(j>=0) && (records[j].key>temp.key);--j)
				records[j+1] = records[j];
		records[j+1] = temp;//填充空位,轮换结束
	}
}
 
void BettQKSort(RecordType records[],int low,int high){
	if(high-low<MIN_CONDITION)
		inser_sortInQK(records,low,high);
	else if(low<high){
		int pos=BettPartition(records,low,high);
		QKSort(records,low,pos-1);
		QKSort(records,pos+1,high);
	}
}

🪴qql1's digital garden

探索

快速排序算法