梗概:

定义:

所有结点的度≤2

性质:

左子树和右子树是有顺序的,
数学性质:
1. 第n层上最多有 $2^{n - 1}$ 个节点
2. 叶结点数=度为2的节点数+1(⭐)
3. 结点总数=叶结点数+度为1的结点数+度为2的结点数

二叉树的五种基本形态

空二叉树
只有一个根结点
根结点只有左子树
根结点只有右子树
根结点有左子树和右子树

特殊的二叉树

斜树
1. 定义: 所有结点都往同一个方向斜
child::满二叉树
child::完全二叉树
child::平衡排序二叉树

二叉树的操作：

常用算法

child::求目标结点的层数算法 child::根据先序序列和中序序列确定唯一二叉树

遍历操作

梗概:

二叉树的基本遍历算法有四种:

先序
中序
后序从三种基本算法中可以衍生出三种遍历算法: 即左右子树遍历顺序交换
逆先序
逆中序
逆后序

两种实现方式: 递归与迭代

基本遍历算法, 都可以用递归和迭代方法实现:

递归最简单, 效率最低
迭代麻烦, 效率高
1. 以下迭代遍历都比较统一
  1. 先序遍历
  2. 中序遍历
  3. 后序相反遍历
    1. 即遍历顺序与后序相反
2. 而后序遍历比较特殊, 比较麻烦

递归层序遍历：

从第一层到最后一层
1. 同一层中，从左到右遍历兄弟结点

递归前序(先序)遍历

图解:

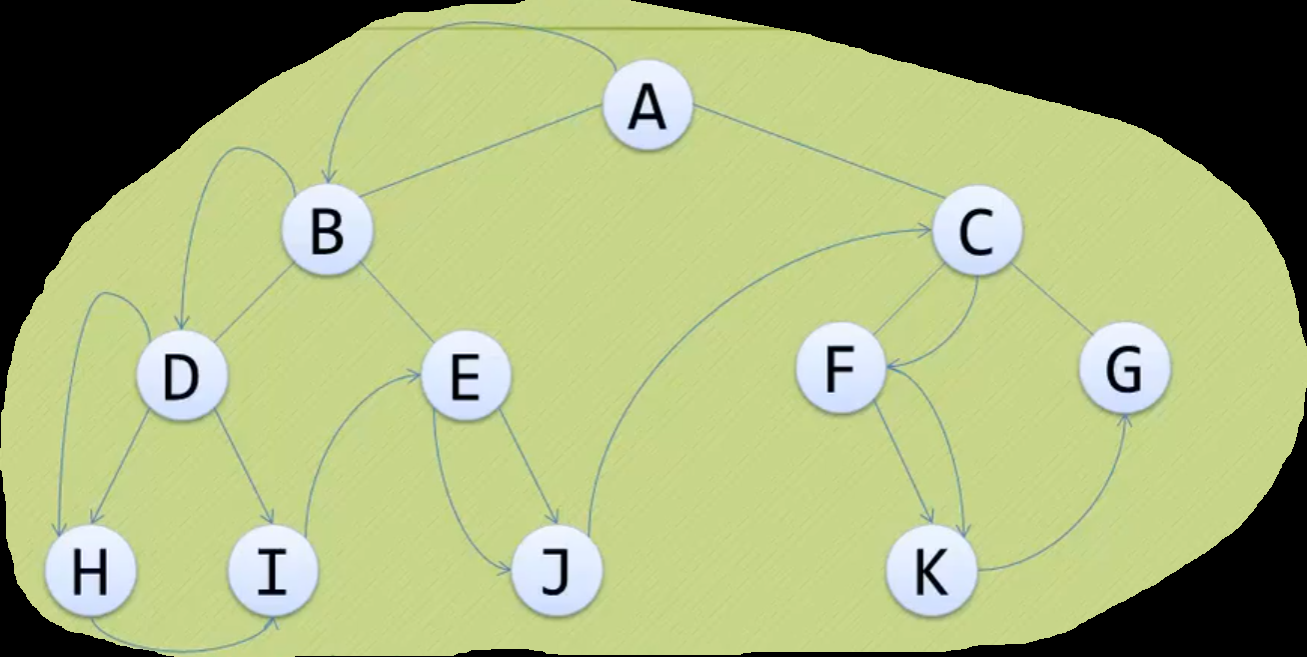
文字描述

把树看成子树嵌套模型
1. 即每棵树都可以看成只有三个结点的树
  1. 其中结点可以是嵌套树, 空结点, 叶子结点
最先遍历根结点
1. 所以叫前序
  1. 前序的序是对每棵树的根结点来说的, 同理, 中序, 后序也是一样的
再遍历左孩子结点
1. 如果左孩子为嵌套树
  1. 则展开该嵌套树, 继续查看左孩子结点,同时遍历左孩子结点(因为是根结点)
    1. 如果还是嵌套树, 继续展开深入, 直到叶子结点
  2. 类似递归的返回过程, 从最下层嵌套树继续套用前序遍历
再遍历右孩子结点
1. 和遍历左孩子一样, 不过是先遍历左孩子再遍历右孩子
遍历完成

递归中序遍历

图解:

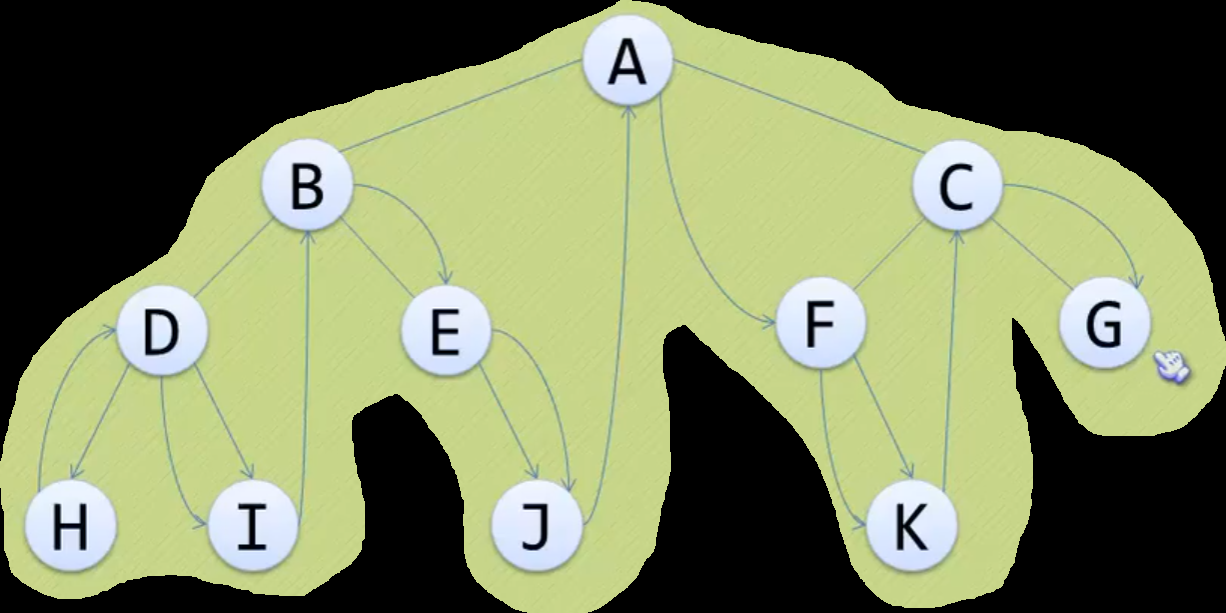
文字描述:

把树看成子树嵌套模型
1. 即每棵树都可以看成只有三个结点的树
  1. 其中结点可以是嵌套树, 空结点, 叶子结点
最先遍历左孩子结点
1. 如果左孩子为嵌套树
  1. 则展开该嵌套树, 继续查看左孩子结点
    1. 如果还是嵌套树, 继续展开深入, 直到叶子结点
  2. 类似递归的返回过程, 从最下层嵌套树继续套用中序遍历
再遍历根节点
1. 所以叫中序遍历
再遍历右孩子结点
1. 和遍历左孩子一样, 不过是先遍历左孩子再遍历右孩子
遍历完成

后序遍历

图解:

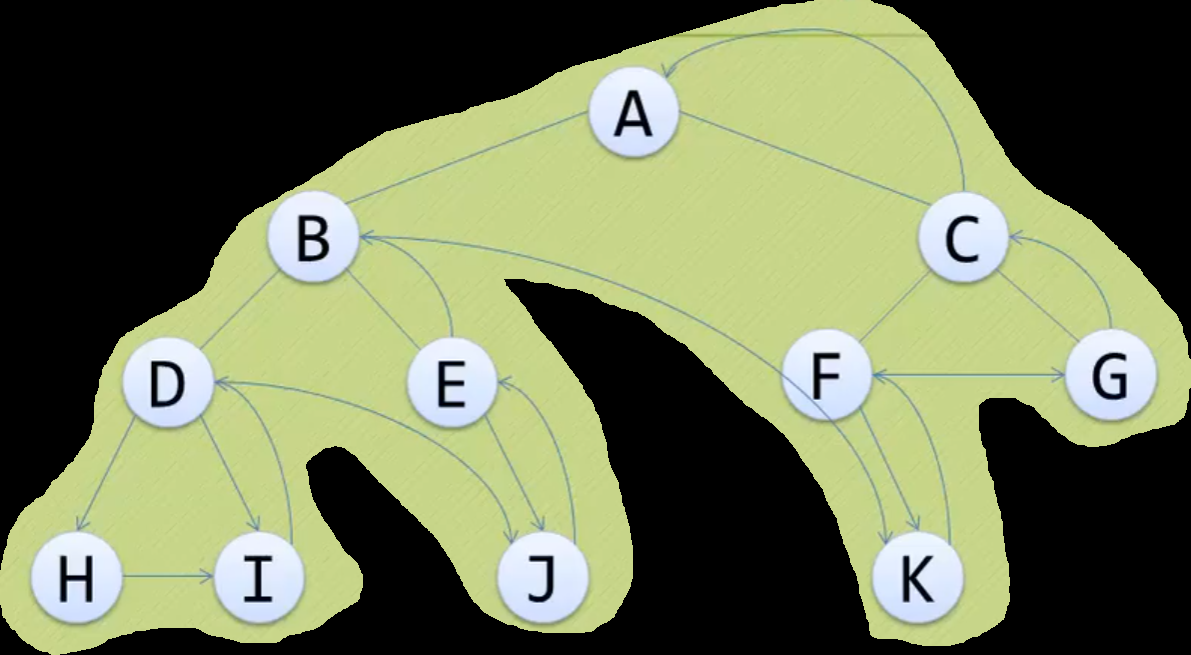
文字描述:

把树看成子树嵌套模型
1. 即每棵树都可以看成只有三个结点的树
  1. 其中结点可以是嵌套树, 空结点, 叶子结点
先遍历左叶子结点(注意不是左孩子结点)
1. 先查看左孩子结点
  1. 如果左孩子为嵌套树
    1. 则展开该嵌套树, 继续查看左孩子结点
      1. 如果还是嵌套树, 继续展开深入, 直到叶子结点
    2. 类似递归的返回过程, 从最下层嵌套树继续套用后序遍历
再遍历右叶子结点
1. 和遍历左叶子结点一样, 不过是先遍历左叶子再遍历右叶子
再遍历根节点
1. 所以叫后序遍历

非递归/迭代先序/中序/反后序遍历:

基本思想:

总结递归的规律, 用栈来模拟递归

迭代先序遍历:

把最靠左的那一列左孩子从上到下入栈, 入完栈再出栈
出栈的时候入栈右孩子, 以及该右孩子中所有靠左的左孩子
入栈的时候操作入栈结点

迭代中序遍历:

与迭代先序遍历框架完全一样, 唯一不同: 出栈时操作出栈结点, 而不是入栈时

5.1.6.4.

迭代反后序遍历

与迭代先序遍历大体相似, 细节相反
1. 把最靠右的那一列右孩子从上到下入栈, 入完栈再出栈
2. 出栈的时候入栈左孩子, 和其所有靠右的右孩子
3. 入栈的时候操作入栈结点

非递归/迭代后序遍历

先找到最左下的最小树,和其最左下的结点, 进行遍历
利用栈回溯双亲以找到右结点, 进行遍历
1. 用栈记录下查看路上所经过的所有双亲结点
  1. 要不然看了左孩子就找不到右孩子了
如果右结点为空, 遍历完左结点直接回溯遍历双亲结点
如果有右孩子, 遍历右孩子
判定从右结点往上回溯双亲, 才进行遍历
1. 需要记录刚刚遍历过的结点, 当其为双亲的右孩子才能遍历(根据后序遍历的顺序)
  1. 因为左孩子和右孩子都有回溯双亲的操作, 需要区分

非递归遍历中序二叉线索树

梗概：
1. 第一个开始遍历的结点在最左下
  1. 分析中序遍历总结的定律
2. 下一个遍历目标就是直接后继

获取输入并创建双链表

默认都是用先序遍历来创建二叉链表, 比起其他顺序, 这种顺序较好

按先序遍历顺序创建二叉链表

获取一个输入数据
把这个数据逐个按照先序遍历顺序放入二叉链表中

求二叉树的高度

分治法求二叉树高度

原理:
1. 二叉树高度=两个子树中得最大高度+1
过程:
1. 子树的高度又用分治法求二叉树高度

先序遍历求二叉树高度

原理:
1. 二叉树高度=所有结点的所对应层次的最大值
  1. 每个结点都有对应的层次
过程:
1. 遍历计数每个结点的对应层次
2. 比较最大值记录和每个结点的对应层次
3. 更新最大值

横向树形显示二叉树

原理:
1. 把树图逆时针旋转90°显示
  1. 用空格作占位符, 占位到对应层级
  2. 根据printf()顺序, 为逆中序遍历根结点
    1. 先打印右子树
    2. 再打印根结点
    3. 再打印左子树
过程:
1. 递归打印右子树
2. 为根结点占位到对应层
3. 打印根结点
4. 递归打印左子树

查找直接前驱:

对中序线索二叉树

梗概:
1. 对于有线索的结点, 直接访问线索即可
2. 对于没有线索的结点, 找左子树的最右下叶结点
  1. 根据中序遍历的顺序总结出来的定律

查找直接后继

对中序线索二叉树

梗概:
1. 对于有线索的结点, 直接访问线索即可
2. 对于没有线索的结点, 找右子树的最左下叶结点
  1. 根据中序遍历的顺序总结出来的定律

二叉树在C语言中的实现:

存储结构梗概:

二叉树有三种存储结构

链式存储结构(最常用)

1. 梗概:

用链表存储所有树结点
每个链结点都设置三个域
1. 左孩子域
  1. 指向左孩子
2. 数据域
3. 右孩子域
  1. 指向右孩子

适用范围:

优点:
1. 内存开销比线索二叉树小一点
缺点:
1. 像单向量链表一样的缺点, 需要从头遍历来找前驱

顺序存储结构

梗概:

按层序遍历把每个结点(包括空结点)放入顺序存储结构中
1. 其中空结点用^表示

适用范围:

优点:
1. 最适合完全二叉树
缺点:
1. 普通二叉树时, 会浪费大量内存

线索二叉树

概述：

线索二叉树根据线索顺序，又可以分为三种线索二叉树
1. 先序线索二叉树
2. 中序线索二叉树
3. 后序线索二叉树
三种线索二叉树结构一样，只不过线索指向不同

通用结构：

每个结点都设置五个域
1. 左孩子域
  1. 左标志域为0时
    1. 指向左孩子
  2. 左标志域为1时
    1. 指向直接前驱
2. 左标志域
  1. 0或1
    1. 1表示没有左孩子
  2. 影响左孩子域
3. 数据域
4. 右标志域
  1. 0或1
    1. 1表示没有右孩子
  2. 影响右孩子域
5. 右孩子域
  1. 右标志域为0时
    1. 指向右孩子
  2. 右标志域为1时
    1. 指向直接后驱

适用范围：

对所有线索二叉树

优点：
1. 把链式二叉树中空的左孩子域和右孩子域利用起来，优化查找直接前驱和直接后继的速度
缺点：
1. 多占用一点空间

对中序线索二叉树

优点：
1. 找直接前驱和直接后继速度平衡
缺点：
1. 找直接前驱和直接后继速度平衡

对后序线索二叉树

优点：
1. 找直接前驱很方便快速
缺点：
1. 找直接后继很困难

对前序线索二叉树

优点：
1. 找直接后继很方便快速
缺点：
1. 找直接前驱很困难

链式存储结构的实现

定义:

typedef struct Node{
DataType data;
struct Node* LChild;
struct Node* RChild;
}BiTNode, *BiTree;
//BiTNode用来定义结点, BiTree用来定义指向根节点的指针

遍历:

递归先序遍历:

梗概:

本质就是深度优先遍历, 也是深度访问当前未访问的邻接点
1. 只不过根结点肯定已访问, 而两个孩子必定未访问代码:

void PreOrder(BiTree root){//root为指向根结点的指针
	if(root!=NULL){
		//对root操作
		PreOrder(root->LChild);
		PreOrder(root->RChild);
	}
}

递归中序遍历:

void InOrder(BiTree root){//root为指向根结点的指针
    if(root!=NULL){
        InOrder(root->LChild);
        //对root操作
        InOrder(root->RChild);
    }
}

递归后序遍历:

void PostOrder(BiTree root){//root为指向根结点的指针
    if(root!=NULL){
        PostOrder(root->LChild);
        PostOrder(root->RChild);
        //对root操作
    }
}

非递归/迭代先序遍历

void PreOrder(BiTree root){
//非递归前序遍历
	SeqStack S;
	InitStack(&S);
	/*用于查看结点的指针*/
	BiTNode* cur;
	/*把左边的左孩子都入栈*/
	for(;root!=NULL;){
		//操作root
		Push(&S,root);
		/*出栈的同时入栈右孩子和其靠左的左孩子*/
		root = root->LChild;
	}
	for(;!IsEmpty(&S);){
		Pop(&S,&cur);
		cur=cur->RChild;
		for(;cur!=NULL;){
			//操作cur
			Push(&S,cur);
			cur=cur->LChild;
		}
	}
}

非递归/迭代中序遍历

void InOrder(BiTree root){
//非递归中序遍历
	SeqStack S;
	InitStack(&S);
	/*用于查看结点指针*/
	BiTNode* cur;
	/*把左边的左孩子都入栈*/
	for(;root!=NULL;){
		Push(&S,root);
		root = root->LChild;
	}
	/*出栈的同时入栈右孩子和其靠左的左孩子*/
	for(;!IsEmpty(&S);){
		Pop(&S,&cur);
		//操作cur
		cur=cur->RChild;
		for(;cur!=NULL;){
			Push(&S,cur);
			cur=cur->LChild;
		}
	}
}

非递归/迭代反后序遍历

void RevPostOrder(BiTree root){
//非递归反后序遍历
	SeqStack S;
	InitStack(&S);
	/*用于查看结点的指针*/
	BiTNode* cur;
	/*把右边的右孩子都入栈*/
	for(;root!=NULL;){
		//操作root
		Push(&S,root);
		root = root->RChild;
	}
	for(;!IsEmpty(&S);){
		Pop(&S,&cur);
		/*出栈的同时入栈左孩子和其靠右的右孩子*/
		cur=cur->LChild;
		for(;cur!=NULL;){
			//操作cur
			Push(&S,cur);
			cur=cur->RChild;
		}
	}
}

非递归/迭代后序遍历

void PostOrder(BiTree root){
//非递归后序遍历
/*p为查看指针,q用来保存已经遍历过的右孩子*/
	BiTNode *p, *q;
	SeqStack S;
	q = NULL;
	p = root;
	InitStack(&S);
	for(;p!=NULL||!IsEmpty(&S);){
		if(p!=NULL){
			/*查看左子树*/
			/*查看的同时保存路上的结点,用于回溯找右孩子和准备遍历*/
			Push(&S,p);p=p->LChild;
		}else{
			/*回溯到双亲结点*/
			GetTop(&S,&p);
			/*遍历了左孩子且没有右孩子=>可以遍历根结点*/
			/*左右孩子都遍历过=>可以遍历根结点了*/	
			if((p->RChild==NULL)||(p->RChild==q)){
				//操作根结点
				/*记录当前所遍历的结点,用于下一次回溯判断*/
				q=p;
				/*遍历完就不需要记录了*/
				Pop(&S,&p);
				/*置空来继续回溯栈顶*/
				p=NULL;
			}else{
				/*还有右孩子没有查看*/
				p=p->RChild;
			}
		}
	}
}

获取输入并创建二叉链表

按先序遍历顺序创建二叉链表

假设结点值为字符类型, 通过getchar()获取输入:

void CreateBiTree(BiTree *bt){
	DataType ch;
	/*假设结点值为字符类型*/
	ch = getchar();
	if (ch=='.') *bt =NULL;
	else{
		*bt=(BiTree)calloc(1,sizeof(BiTNode));
		(*bt)->data=ch;
		CreateBiTree(&((*bt)->LChild));
		CreateBiTree(&((*bt)->RChild));
	}
}

以下创建测试用二叉树:
1. 横向打印:
```
  F
 D
  E
A
 B
  C
```
2. 输入: ABC…DE..F..

求二叉树的高度

分治法求二叉树高度

int PostTreeDepth(BiTree bt){
	int hl, hr, max;
	if (bt==NULL) return 0; //递归出口
	hl = PostTreeDepth(bt->LChild);
	hr = PostTreeDepth(bt->RChild);
	max = hl>hr?hl:hr;
	return max+1; //子树高度最大值+1就是当前树高度
}

先序遍历求二叉树高度

int depth;
void PreTreeDepth(BiTree bt, int h){//h记录当前所在层
	/*h为bt指向结点所在层次，初值为1*/
	/*depth为当前求得得最大层次，为全局变量，初值为0*/
	if(bt==NULL) return ;
	if(h>depth) depth=h;//如果大于,更新depth
	PreTreeDepth(bt->LChild,h+1);//h+1以迭代hd
	PreTreeDepth(bt->RChild,h+1);
}

横向树形显示/打印二叉树

void PrintTree(BiTree bt,int nLayer){//顶树的层应为0
	//nLayer为根结点所在层次
	if(bt==NULL) return;
	/*打印右子树*/
	PrintTree(bt->RChild,nLayer+1);
	/*占位到对应层*/
	for (int i=0;i<nLayer;i++)printf(" ");
	/*假设结点数据类型为字符*/
	/*打印根*/
	printf("%c\n",bt->data);
	/*打印左子树*/
	PrintTree(bt->LChild,nLayer+1);
}

中序线索二叉树的实现

线索二叉树的定义:

typedef enum {link,Thread} PointerTag;
typedef struct Node{
	DataType data;
	struct Node *LChild, *RChild;
	PointerTag Ltag;
	PointerTag Rtag;
}BiThrNode, *BiThrTree;

二叉树中序线索化

BiThrNode* pre;
void Inthread(BiThrTree root){
	/*采用中序遍历对根结点加线索*/
	/*pre为全局变量,为上一次访问的结点,初值为NULL*/
	if(root==NULL)return;//遍历出口
	Inthread(root->LChild);
	/*加线索操作*/
	if (root->LChild==NULL){
		/*置直接前驱线索*/
		root->LChild=pre;root->Ltag=1;
	}
	if (pre!=NULL&&pre->RChild==NULL){
		/*置直接后继线索*/
		pre->RChild=root;pre->Rtag=1;
	}
	pre=root;
 
	Inthread(root->RChild);
}

在线索二叉树中查找直接前驱

BiThrNode *InPre(BiThrNode *p){
	//查找p的直接前驱,并用pre指针返回
	if(p->Ltag==1) pre=p->LChild;
	else {
		/*在p左子树中查找最右下的叶结点*/
		for (p=p->LChild;p->Rtag==0;p=p->RChild);
		pre=p;
	}
	return(pre);
}

在中序线索二叉树中查找直接后继

BiThrNode * InNext(BiThrNode *p){
	//查找p的直接后继,用Next指针返回
	BiThrNode *Next;
	/*直接利用线索*/
	if(p->Rtag==1) Next=p->RChild;
	else {
		/*在p的右子树中查找最左下的叶结点*/
		for(p=p->RChild;p->Ltag==0;p=p->LChild);
		Next=p;
	}
	return Next;
}

非递归遍历中序线索二叉树

void TInOrder(BiThrTree Bt){
	BiThrNode *p=Bt;
	/*在最左下查找遍历开始结点*/
	if(!p)return 0;
	for(;p->Ltag==0;p=p->LChild);
 
	for(;p;){
		//对p操作
		
		/*遍历直接后继*/
		if(p->Rtag==1) p=p->RChild;
		else {
			for(p=p->RChild;p->Ltag==0;p=p->LChild);
		}
	}
}

在JavaScript/ts中的实现:

链式存储结构:

横向打印/显示二叉树:

PrintTree(root=this.root,layer=0){
	if(!root)return false;
	/*打印右子树*/
	this.PrintTree(root.RChild,layer+1);
	/*为根结点占空位到对应层次*/
	for(let i=0;i<layer;++i)process.stdout.write('  ');
	process.stdout.write(root.key+'\n');
	/*打印左子树*/
	this.PrintTree(root.LChild,layer+1);
}

注:

需要使用node. js

🪴qql1's digital garden

探索

二叉树

梗概:

定义:

性质:

二叉树的五种基本形态

特殊的二叉树

二叉树的操作：

常用算法

遍历操作

梗概:

两种实现方式: 递归与迭代

递归层序遍历：

递归前序(先序)遍历

图解:

文字描述

递归中序遍历

图解:

文字描述:

后序遍历

图解:

文字描述:

非递归/迭代 先序/中序/反后序遍历:

基本思想:

迭代先序遍历:

迭代中序遍历:

5.1.6.4.

非递归/迭代后序遍历

非递归遍历中序二叉线索树

获取输入并创建双链表

按先序遍历顺序创建二叉链表

求二叉树的高度

分治法求二叉树高度

先序遍历求二叉树高度

横向树形显示二叉树

查找直接前驱:

对中序线索二叉树

查找直接后继

对中序线索二叉树

二叉树在C语言中的实现:

存储结构梗概:

链式存储结构(最常用)

1. 梗概:

适用范围:

顺序存储结构

梗概:

适用范围:

线索二叉树

概述：

通用结构：

适用范围：

对所有线索二叉树

对中序线索二叉树

对后序线索二叉树

对前序线索二叉树

链式存储结构的实现

定义:

遍历:

递归先序遍历:

递归中序遍历:

递归后序遍历:

非递归/迭代先序遍历

非递归/迭代中序遍历

非递归/迭代反后序遍历

非递归/迭代后序遍历

获取输入并创建二叉链表

按先序遍历顺序创建二叉链表

求二叉树的高度

分治法求二叉树高度

先序遍历求二叉树高度

横向树形显示/打印二叉树

中序线索二叉树的实现

线索二叉树的定义:

二叉树中序线索化

在线索二叉树中查找直接前驱

在中序线索二叉树中查找直接后继

非递归遍历中序线索二叉树

在JavaScript/ts中的实现:

链式存储结构:

非递归/迭代先序/中序/反后序遍历: