二重积分的换元法

1. 实际经验运用:

1. 常用换元模型:

1.1. 原积分区域为椭圆,

1.1.1.1. 令x=aρcosθ, y=bρsinθ

1. 以消去a和b, 积分区域变成极坐标里面的圆
2. 雅克比行列式恒等于abρ

2. 适用范围:

1. 二重积分换元法前提条件:

1.1. 一般都成立的前提条件:

1. x=x(u,v) 和 y=y(u,v)一阶偏导存在
2. 在一小块面积上的雅克比行列式!=0
   1. 如果雅克比行列式只在一个点或线上为零, 则依然满足前提条件
3. 换元后的点只和原来的点只能一对一

2. 需要用到换元法的情景:

1. 被积函数不好积
2. 积分区域比较复杂, 不好表示

3. 相关概念:

1. 雅克比行列式:

1.1. 符号记法

1.2. 计算公式:

对二重积分f(x,y),和两条换元方程:

1. x=x(u,v)
2. y=y(u,v) 则公式为:

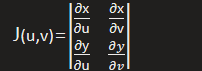
2. 极坐标二重积分就是二重积分换元法的一个特例

其中x和y都换成ρ和θ, 雅克比行列式恒为ρ, 积分区域不变

4. 换元公式:

5. 注意点:

1. 雅克比行列式有绝对值 积分区域改变

6. 使用换元法的详细步骤:

1. 确定后要把什么换成u和v,得到两条方程
2. 对上面两条方程, 分别把x和y作为因变量, 放在等号一边
3. 变换积分区域,
   1. 通过两条换元方程,
   2. 把原积分区域的所有包围曲线用u和v的方程表示出来
4. 计算雅克比行列式
5. 在新的积分区域上确定两层积分的上下限
6. 代入换元法公式中计算二重积分