高数下十一 4 无向曲面的积分

对面积的曲面积分

计算步骤:

1. 先看积分区域对称性
   1. 包括奇偶性和轮换对称性
   2. 再看被积函数奇偶性 3. 把被积函数按加减法拆分后再看奇偶性
2. 再看能不能使用形心/质心公式把变量提出去
3. 看看联立被积函数和积分区域看看能不能化简式子
4. 看看几何意义计算法
5. 看看特殊换元法
6. 看看投影法

定义:

积分区域为无向曲面

符号记法:

1. 特殊的符号记法:

积分区域为闭合曲面:

运算规律:

1. 符合常识的运算规律:

1. 可拆合性
2. 常数可外提

2. 不符合常识的运算规律:

1. 单独变量往外提变成对应平均值

性质:

1. 奇偶性: 若曲面Σ关于xoy对称
2. 如被积函数关于z为偶函数 则曲面Σ对称的两半相等
3. 如被积函数关于z为偶函数 则曲面Σ对称的两半互为相反数, 即该曲面积分为0

计算方法:

1. 投影转二重积分法:

1.1. 前提:

1. 投影面积!=0
2. 曲面的投影面不能有重叠 需要分割成没有重叠的若干部分

1.2. 步骤:

1. 根据需求投影在某个坐标面上(以xoy平面为例)
2. 联立曲面方程消元被积函数
   1. 消掉投影坐标(z)
3. 
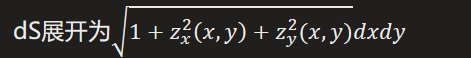
   1. 对应无向曲线的微分元展开式, 只不过投影坐标(z)的导数恒为1罢了
4. 积分区域变为投影面

2. 曲面积分的特殊换元法:

2.1. 换元为球面坐标:

1. 对应坐标换元
2. dS展开为r²sinφdθdφ
   1. 与二重积分的dv展开区分: 少一个dr
      1. dv=r²sinφdrdφdθ

助记:

1. 因为是面积元, 所以比体积元少一个高, 即少一个dr
2. 积分区域不变

3. 几何意义计算法:

3.1. 按简单几何意义展开dS为其他微分量

如dS= d长·d宽 这样就会变成二重积分了

计算技巧:

1. 联立曲面方程和被积函数来化简式子 2. 原理:被积函数与积分区域的关系
2. 用轮换对称性合并变量
   1. 相关概念: 轮换对称性
3. 形心/质心/重心公式:
   1. 相关概念: 形心质心重心公式