梯度

1. 梯度的应用:

1. 用梯度求二元函数某一点的法向量

1.1. 例:

1.1.1.1. 解析:

二元函数图形就是构造的三元函数的某一个等值面 二元函数图形的法向量就是构造的三元函数的梯度

1.1.1.2. 解:

1. 移项(把常数和自变量分开放到等号两边): z-x²-y²=9
2. 构造三元函数:
   1. 令F=z-x²-y²
3. 

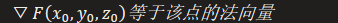
2. 相关概念:

1. 等值图形:

1.1. 直观理解:

1. 对一元函数(二维函数), 有等值点(一维)
2. 对二元函数(三维函数), 有等值线(二维)
3. 对三元函数(四维函数), 有等值面(三维) 以此可以类推高维函数的等值图形 n维函数有(n-1)维的等值图形

1.2. 形式:

dd故任何函数都等于更高维函数的等值图形(⭐)

1.3. 性质:

1. 在函数内某一点, 经过该点的等值图形唯一(⭐)

3. 直观理解(几何意义):

1. 对二元函数(三维函数)的梯度:

梯度是投影在自变量平面(二维)内的一个向量

1. 该向量的方向为方向导数取最大值的方向
   1. 该向量的大小(模)为方向导数的最大值
2. 对某一点, 梯度垂直于该点所在的等值线.

2. 对高维(n维)函数的梯度:

1. 梯度为投影在(n-1)维的一个向量
2. 对某一点, 梯度垂直于该点所在的等值图形

2.1. 应用:

已知一个n维的函数, 求某一点的法线

1. 这个函数就是维n+1维函数的等值图形

4. 定义:

梯度是一个向量

5. 梯度符号记法:

1. 
2. 

6. 梯度与方向导数的关系:

对某一点, 在某一方向l.

1. 方向导数=梯度·$e_l$(⭐)
2. 方向导数=|梯度|cosθ , (θ为梯度和方向l的夹角)

7. 梯度性质:

关于θ的性质:

1. 当θ=0时, 方向导数取最大值, 即梯度的模
2. 当θ=π时, 方向导数等于负的梯度模
3. 当θ=π/2 ,方向导数=0, 即这个方向函数值不变