二重积分

1. 相关概念：

1. 直径：

1.1. 定义：

图形中任意两点距离的最大值

1.2. 符号记法：λ

2. 二重积分的几何意义：

类似普通积分的结果为面积，二重积分的结果为顶曲面圆柱体的体积 即顶曲面竖直往xoy平面延伸形成的柱体

1. 二重积分正负的规定：

类似普通积分 顶曲面在xoy平面以上, 为正, 在下, 为负

3. 二重积分定义：

1. ∆σ表示任意形状的小块面积
2. 

1. 面积元素的选取：

理论上∆σ可以是任意形状，

但为了计算方便, 做题取dσ只有两种模式

1.1. 对直角坐标系

1. dσ为平行x轴和平行y轴的线构成的图形
   1. (即把积分区域横着切, 竖着切)

4. 二重积分符号记法:

1. D可以是其他符号, 用来表示二重积分的范围
2. dσ表示面积元素, 表示两个自变量构成的极微小面积

5. 二重积分的条件：

函数有界 ⇒ 可二重积分

1. 二重积分性质:

1. 符合常识:

1. 常数可往外提
2. 积分内加法可拆分
3. 积分区域可拆分
4. 积分后大小不变
5. 上减下求两曲面构成的柱体体积 在一定区域内, 该柱体体积=(上曲面减下曲面)的二重积分
6. 二重积分中值 即积分区域内存在一点, 他的函数值为这个区域的平均函数值

2. 不符合常识的性质:

1. 先求绝对值再积分数值更大

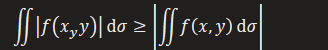
二重积分的计算

• child::直角坐标二重积分的计算
• child::极坐标二重积分的计算
• child::二重积分的换元法

9. 二重积分的特殊应用:

child::求平面图形面积